AtCoder Beginner Contest 248 F問題 Keep Connect
問題
提出解答
問題の概要
無向グラフ を以下で定義する.
それぞれに対して, 次を満たす
の全域部分グラフ
の個数を求め,
で割った余りを求めよ.
は連結
制約
は素数
解法
以降では説明のために, 本の辺をそれぞれ
と名付けることにする.
動的計画法で解くことにする. に対して,
を以下を満たす場合の数で定義する.
- 考えるグラフを
の
から生成される部分グラフに制限したとき, 取り除かれた辺の本数が
で,
のとき: 連結であるような全域部分グラフの数
のとき: 連結成分がちょうど2つであり,
が非連結であるような全域部分グラフの数.
ベースケースを考える. 今回のベースケースは のときであり, この場合に考えるべき辺は
のみである. これらを残すか残さないかどうかで考えることにより,
である.
更新式を考える. まで決定している状況で
の状況を決定づけるためには, 新たに
を残すかどうかの判定をすればよい. このとき, 以下の表を利用することにより, 遷移がを求めることができる (ただし, 青数字は
のうち,残さなかった辺の数を表す).
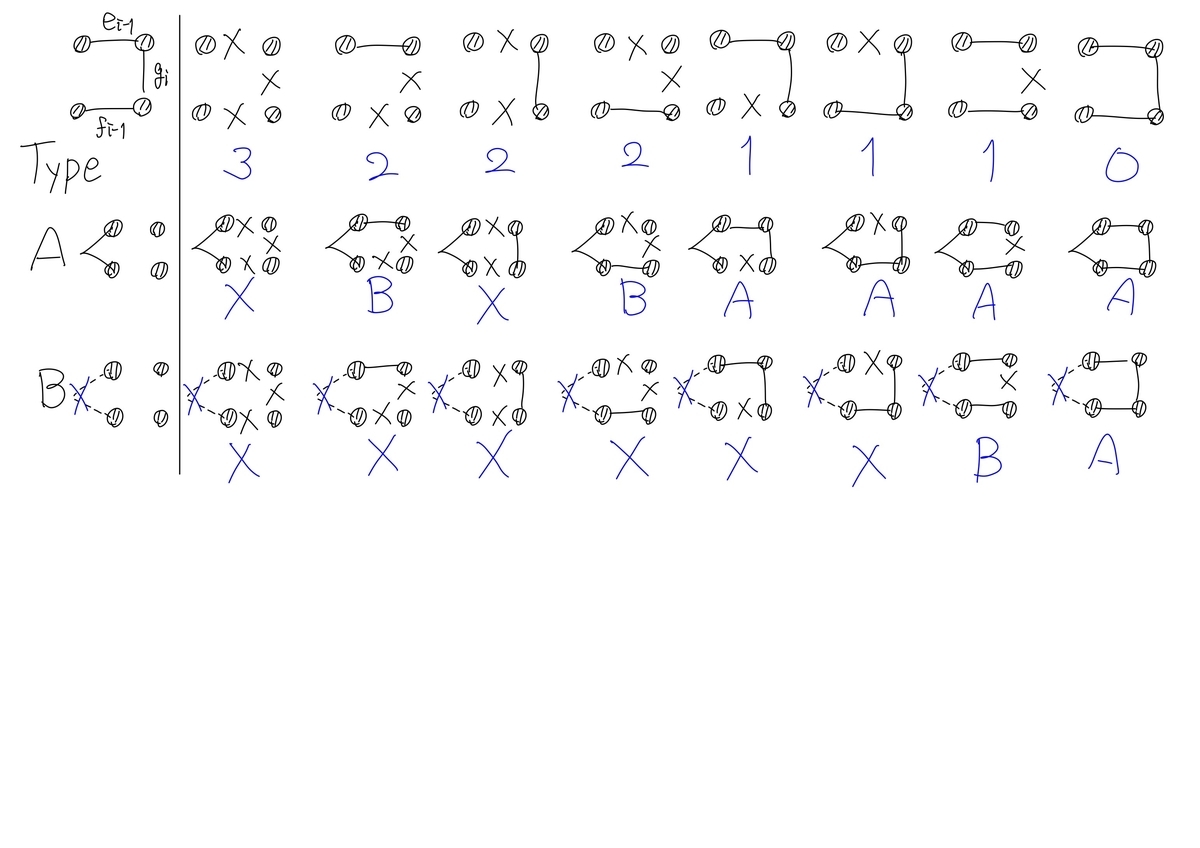
このとき, 答えは である. 配列の要素数は
で, 各要素の更新は定数時間でできるので, 全体の計算量は
である.